【技术交流】裂隙地下水渗流及溶质迁移数学模型研究进展
裂隙地下水渗流及溶质迁移数学模型研究进展
摘要：针对裂隙地下水渗流及溶质迁移多场耦合数学模型，综述模型研究的发展历程与阶段性成果，将现有模型划分为基于不同介质概化的等效孔隙介质模型、多重介质模型、离散裂隙模型，基于不同耦合方法的非全耦合模型与全耦合模型，以及基于不同模型推导途径的力学途径模型与混合耦合理论模型。针对该领域研究的关键科学问题总结其发展趋势，探讨裂隙地下水渗流及溶质迁移多场耦合数学模型研究的难点及潜在发展方向，为裂隙地下水流及溶质迁移研究提供理论参考。
关键词：裂隙岩体；地下水；耦合模型；渗流；溶质迁移
裂隙岩体中的渗流与溶质迁移研究对于很多领域十分重要，例如裂隙含水层地下水修复、油气开采与地下工程建设等[1-3]。长期以来，孔隙介质假设在饱和非饱和地层中地下水渗流、化学溶质迁移中得到广泛应用，然而许多岩石中发育极多裂隙，裂隙实际上控制了渗流过程，相比于理想孔隙介质而言具有很多不同的特征[4-5]。另一方面，由于岩石总是处在一定的地质环境之中，对于其渗流及溶质迁移的研究必须考虑到其他控制性物理场的共同作用[6-7]。高度不均匀的参数分布、裂隙与孔隙间的相互影响以及多物理场之间的复杂耦合作用是裂隙地下水渗流及溶质迁移研究的突出难点。复杂的裂隙分布往往导致裂隙地下水的监测、分析都存在较大困难，模拟仿真使得裂隙介质渗流与溶质迁移多物理场耦合现象的研究成为可能，目前已经成为重要的研究手段[1, 8-10]，模拟仿真的基础是数学模型。国内外相关学者基于不同的介质假设、不同的物理场耦合方法等提出了多种模型。为了相关研究工作的持续开展，有必要结合不同研究思路及其研究特点，综述国内外研究学者对于裂隙地下水渗流及溶质迁移多场耦合模型研究的阶段性成果及研究历程，为裂隙地下水模型的进一步研究提供参考。
1 裂隙地下水模型的介质概化
裂隙地下水渗流与溶质迁移模型需要表征裂隙的存在对于渗流的影响，按照对裂隙介质的概化方法可分为等效孔隙介质模型、多重介质空间模型、离散裂隙模型等，不同的模型类型适用于不同的研究情景。
1.1 基于等效孔隙介质假设的模型
等效孔隙介质模型是最简单的连续介质模型，通常应用于超大尺度计算中[11]。在该类模型中，通过调整多孔介质的渗透率来表达裂隙对于整体介质的影响。由于裂隙在空间中分布特征与填充程度、岩性的不同，调整后的渗透率可能增大，也可能减小，不同方向的渗透率相对大小也发生改变，用以表示裂隙介质中的高度非均质性。通过对一定大小的介质空间进行计算，最终获取整个裂隙化多孔介质的等效渗透率。因此，对于某一特定尺寸的介质空间，其等效渗透系数[12]可以表示为：
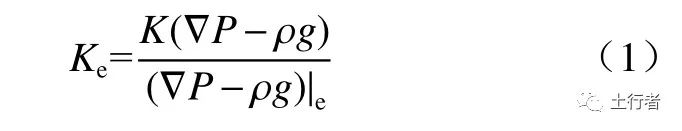
式中：K为介质空间内某点的渗透系数，m2；K(∇P-ρg)代表特定大小（同时包含孔隙与裂隙特征单元）介质空间内的平均渗流速度，m/s；(∇P-ρg)|e为等效压力梯度，Pa/m。使用等效渗透率这一概念实际上使得模型蜕化为类似于普通孔隙介质模型的简单模型，计算简单方便，因此其应用非常广泛。冯金德等[13]和高丽等[14]通过利用平行板理论、张量理论确定了天然裂隙参数对储层等效渗透率的影响。然而对于更复杂的问题，比如可压缩流体运移等，确定等效渗透率往往是较为困难的，同时等效孔隙介质模型无法捕捉到裂隙与孔隙流动的不同特征，对于渗流场、浓度场等刻画太过简单，模型有效性常常受到质疑[15-16]。
1.2 考虑裂隙分布的模型
为更加精细地考虑裂隙发育对于计算的影响，进而研究高度不均匀的储存空间特征与孔隙空间-裂隙空间复杂的相互作用[5]，必须考虑裂隙岩体中裂隙流与孔隙流的显著区别，解决这一类问题的模型可划分为等效多重介质模型（仍基于连续介质假设）与离散裂隙模型。
1.2.1 等效多重介质模型
等效多重介质模型是一类用多种介质相互重叠来表示裂隙化多孔介质的模型，这些不同的介质使用各自的均衡方程和传输定律，其中最为常见的是等效双重介质模型（图1）。固体颗粒与颗粒之间的小孔隙组成孔隙基质，而孔隙基质与裂隙空间组成了更高一级多孔介质。
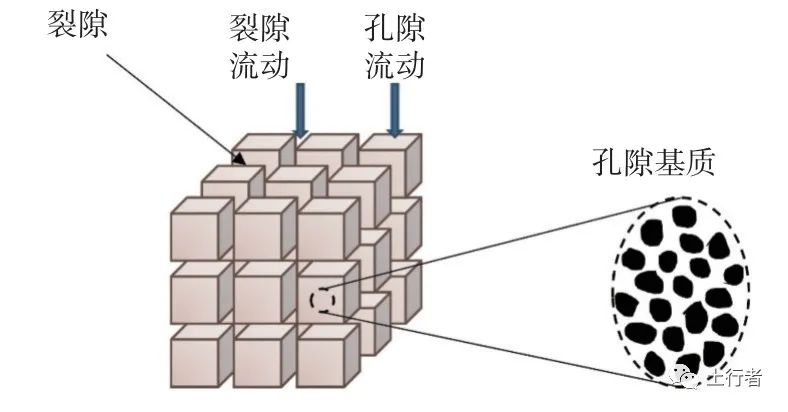
图1 双重介质空间
Fig.1 Conceptual description of dual porosity media
等效双重介质模型最初由Barenblatt等[17]提出，裂隙和孔隙作为两个相对独立的连续相，在岩石中的任意位置均存在裂隙与孔隙对应的物理量。之后，Warren等[18]针对双重介质假设进行了改进，使得模型可以更好地表征裂隙化岩石存在的非均质性。双重介质模型的渗流控制方程为：
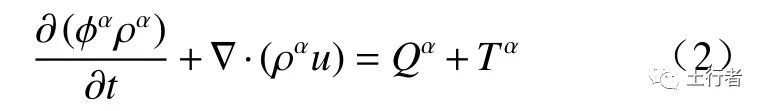
式中：φα为 空隙度（α可 表示孔隙或裂隙）；ρα为流体密度，kg/m3；u为流速，m/s；Qα为 源汇，kg/(m3·s)；Tα为孔隙-裂隙交换量，kg/(m3·s)。由于孔隙与裂隙共同组成裂隙化岩石，因此有：
式中：φ为岩石总空隙度。孔隙-裂隙交换量的计算是等效双重介质模型的一个关键。Kazemi等[19]在针对裂缝性油藏的研究中考虑了均匀分布和非均匀分布的裂缝，忽略了孔隙中的流动，只模拟裂隙中的渗流。Musso等[20]在对压实黏土的化学-水-力学耦合行为的双重介质空间研究中同样忽略了微孔中的流动。上述模型一般被称作单渗透率模型，此时孔隙作为裂隙的源，只发挥储存体积作用而不发挥渗流通道作用，孔隙空间控制方程为：
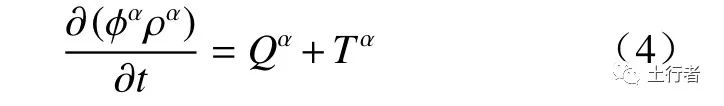
式中符号含义同前。单渗透率模型只在孔隙基质与裂隙空间渗透率相差极大，且孔隙基质内流动可以忽略时适用。近年来，研究者们一般采用双渗透率模型，也即孔隙介质和裂隙空间均考虑渗透作用。Khalili[21]在研究中同时考虑了孔隙与裂隙中气液两相流体的渗流，这使得孔隙-裂隙渗流交叉影响的研究成为可能。Li等[22]在MX-80膨润土的研究中，使用了同时考虑微孔与大孔渗透的双重孔隙模型，确定了溶质浓度对微孔尺度上力学变形的影响。按照是否与时间成显式关系可将交换量的计算方法分为稳态与瞬态两种。对于稳态计算方法，交换量与孔隙-裂隙间的压力差成正比[18]，即：
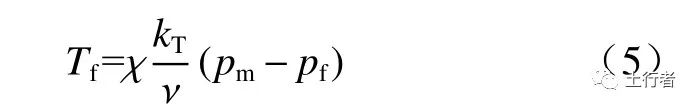
式中：T f为孔隙向裂隙的体积交换量，m3/s；χ为裂隙形状系数，与裂隙的间距、维度、渗透性有关，m；kT为交换过程中的渗透率（孔隙或裂隙渗透率），m2；ν为动力黏滞系数，kg/(m·s)；pm与pf分别为孔隙与裂隙流体压力，Pa。对于瞬态计算方法，交换量实际上通过孔隙与裂隙渗透控制方程计算求得，交换量与时间成显式关系。Zimmerman等[23]使用了非线性计算公式计算瞬态交换量，研究结果显示瞬态算法能够降低在数值求解过程中的误差。总的来说，稳态方法从原理上相当于非稳态方法的近似，可看作非稳态方法长期计算后的解，但相比于非稳态方法其计算较为简单，应用更加广泛。
1.2.2 离散裂隙模型
离散裂隙模型是一种对裂隙进行显式刻画的模型，一般需要确定每条裂隙的空间方位、间距、填充等参数，以单裂隙内水流计算为基础，计算所有裂隙内渗流，进一步获取整个渗流空间内每一点的流体压力。根据是否考虑孔隙基质渗透作用，离散裂隙模型可进一步分为离散裂隙基质模型（discrete fracture matrix model ，DFM）与离散裂隙网络模型（discrete fracture network model，DFN）。DFM认为流体既存在于裂隙中，也存在于孔隙基质中，根据裂隙的不同长度与特征，裂隙可被处理为孔隙基质的内部结构，也可被处理为普通裂隙[24]，由于保留了孔隙空间，该模型可用于研究孔隙-裂隙的复杂界面作用。Lee等[25]进行了自然裂缝分层建模，将裂缝按不同级别进行表征，既研究了中长裂缝的对基质有效渗透率的影响，又成功捕捉了被明确为主要流体管道的长裂缝。离散裂隙网络模型（DFN）则认为孔隙基质对于整体计算并不重要，因此在DFN模型中，假设所有流体都储存在裂隙网络中，通过计算各裂隙交点的流体压力值获取整体渗流空间特征。Gao等[26]的研究表明了三维DFN模型可以灵活地表征裂缝分布，使得构建离散裂缝网络更容易、更快捷。DFN模型可以准确地描述裂隙内的流体动力学，对于多物理场耦合计算具有优势。
2 裂隙地下水多物理场耦合模型
裂隙岩体中地下水渗流与溶质迁移分别受到渗流场与溶质浓度场的控制，并受到其他物理场的强烈影响。按照不同物理场之间是否完全双向耦合，多物理场耦合模型一般可划分为全耦合模型与非全耦合模型。除此之外，还可分为边界耦合和域耦合、直接耦合与间接耦合、同质耦合与异质耦合、微分耦合与代数耦合等[27]。
2.1 非全耦合模型
非全耦合模型一般指不同物理场控制性偏微分方程只是松散连接，独自求解后通过交换关联变量实现相互影响的模型。部分模型在处理耦合时只考虑物理场之间的单向影响，也属于非全耦合模型。
2.1.1 渗流-化学溶质场耦合
经典的多孔介质溶质迁移模型属于非全耦合模型，溶质的迁移决定于多孔介质内流体的运动及溶质浓度场梯度，其一般形式的方程[28-29]为：
式中：k为渗透率，m2；krl为 相对渗透率；Cs,p为以压力表示的特定湿度比值，m·s2/kg；Kl为流体体积模量，Pa；p为流体压力，Pa；Sl为 流体饱和度；cc为溶质质量分数；D为溶质扩散系数，m2/s。该类模型在孔隙裂隙介质污染物迁移转化等研究中已经得到了广泛的应用[2, 3]。值得注意的是，模型实际上只考虑了溶质在流体中的对流与弥散作用，忽略了溶质浓度场对于渗流场的影响（如密度变化、化学渗透等）。Chen等[30]和 Schlemmer等[31]的研究已经表明，在低渗透性的岩石（如裂隙岩体的孔隙基质）中由于溶质浓度导致的化学渗透是非常重要的，忽略化学渗透可能带来显著的误差。
2.1.2 渗流-力学场耦合
地下水在岩石中的流动受到岩石变形的影响，研究渗流-力学场的耦合模型一般被称为固结模型。太沙基一维固结理论是经典的渗流-力学场非全耦合模型。20世纪20年代，太沙基首先基于7个关于饱和土有侧限小应力应变问题的假设提出了解决一维岩石力学场-渗流场耦合计算问题的理论。根据太沙基有效应力原理，对于饱和土体，其有效应力[32]为：
式中：σ＇为 土体有效应力，Pa；p＇为外部荷载造成的额外孔隙水压力 (超孔隙水压力)，Pa；σt为总应力，Pa。对于土体中深度为z的一个微元体，根据达西定律和微元体体积守恒有：
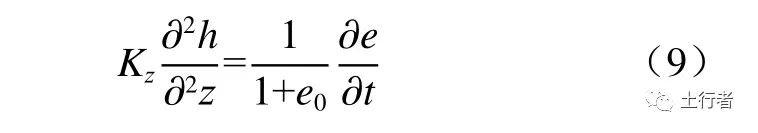
式中：h为 深度为z处的孔隙水压力水头，m；Kz为z方向的渗透系数，m/s；e0为初始孔隙比；e为固结过程中任意时刻的孔隙比。结合饱和土体孔隙比与有效应力的关系可得太沙基一维固结方程为：
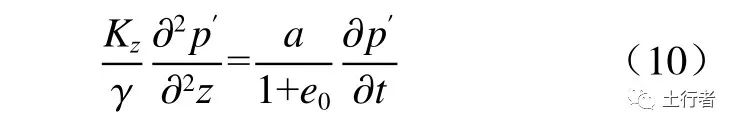
式中：γ为水的重度，kg/（m2·s2）；a为岩石固结系数，m·s2/kg。
2.2 全耦合模型
全耦合模型的建立需要考虑某一具体现象的全部控制性物理场，建立全体变量的耦合方程组。以热力场-力学场-渗流场-化学场的四场全耦合行为为例（图2），模型需要考虑：渗流-力学、渗流-热力、渗流-化学、力学-热力、力学-化学、热力-化学之间的双向耦合关系。因此，一般来讲，全耦合模型涉及的方程组均为大型偏微分方程组，求解相对复杂，但其对于物理现象的描述最为精确，是其他模型所不能替代的。
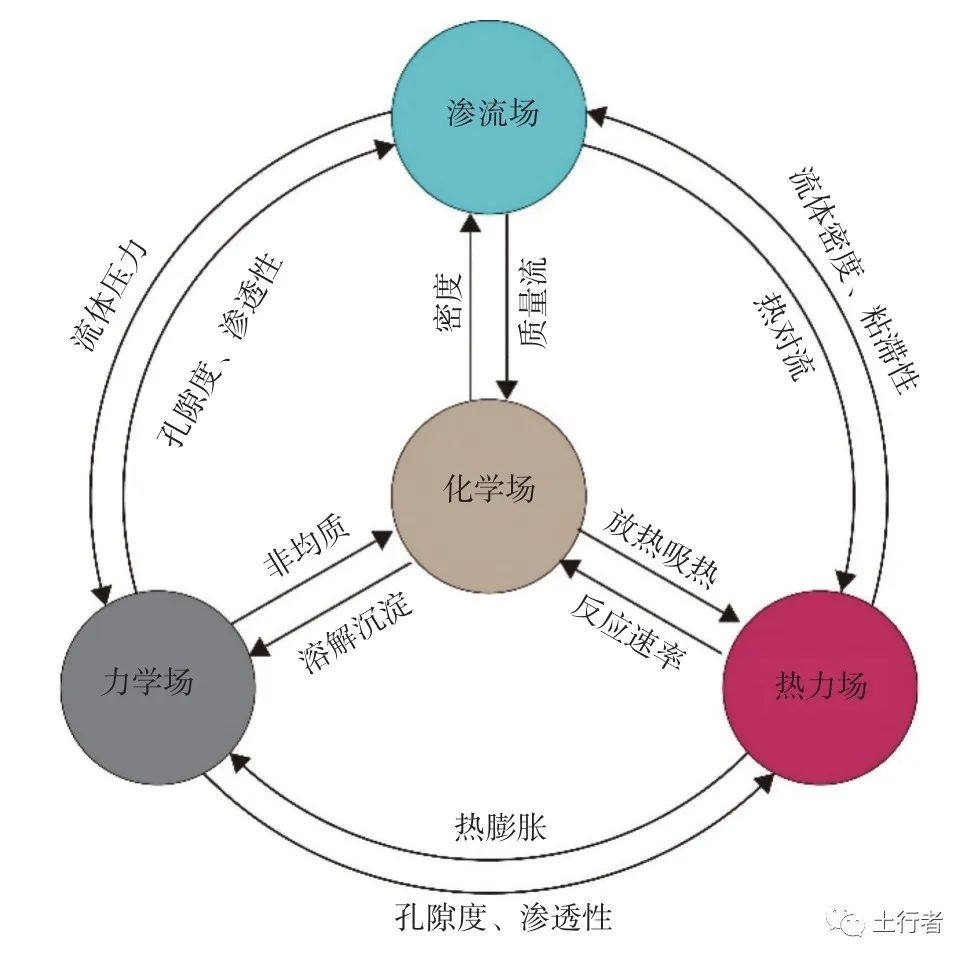
图2 多物理场耦合效应
Fig.2 Conceptual description of multi-physics coupling
2.2.1 力学途径全耦合模型
力学途径建立的全耦合模型是在岩石受力平衡、流体质量均衡、动量守恒等基本原理基础上建立的，该类模型可以通过引用不同学科的偏微分方程来实现对于耦合场的全覆盖，但最初的应用仍然是在渗流-力学场的耦合[34]。渗流-力学场三维全耦合模型研究始于Biot[35]。基于7条关于三维固结问题的假设，考虑一个代表性微元体，根据弹性变形假设可得孔隙水压力、位移和应变的表达式[35]：
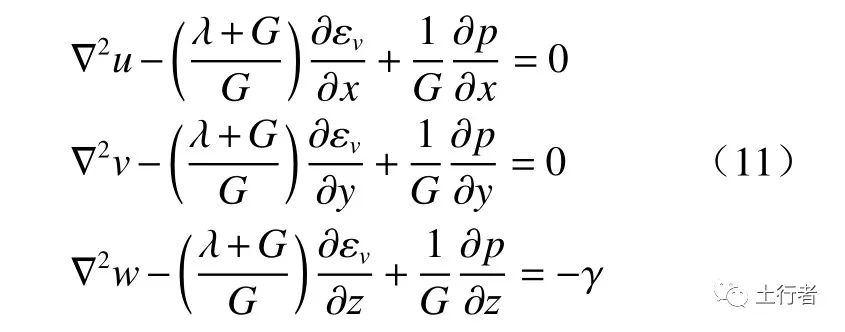
式中：u,v,w为 岩石3个方向的变形位移，m；λ=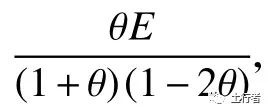
Pa；εv=εx+εy+εz，为体积应变。E和G为弹性模量和剪切模量，Pa；θ为泊松比。水压力与力学方程为：
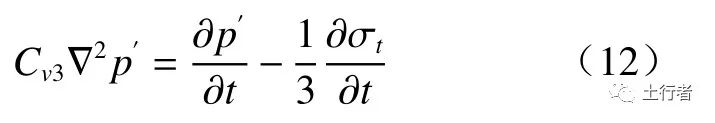
式中：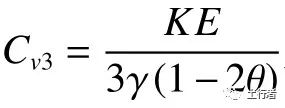
为三维固结系数，m2/s。式(12)与式(11)组成了Biot三维固结理论。求解该方程组可以获得同时满足应力-应变关系、平衡方程和地下水渗流的解，该模型在一维假设条件下简化后可以退化为太沙基一维固结方程的形式。青少年正处在身体发育及成长的关键阶段，其健康的饮食习惯，不仅能保证身体所需的各种营养物质的提供和吸收，也可以杜绝不良饮食习惯给身体造成的伤害。近20年来，渗流-力学场耦合模型的研究和发展以及模型的实际应用大多是在地下水开采、地面沉降、油气勘探、干热岩石地热能调查和核废料处理研究等方面进行的[6, 7, 36, 37]。在Biot之后，研究者们[38-40]基于Biot理论改进了岩石变形方程，用以研究大变形或弹塑性变形下渗流-力学耦合行为。对于较大的变形，渗透率随孔隙度的变化不可忽略，Meroi等[41]在研究中调整了渗透率的方程，渗透率不仅是含水饱和度的函数，也是孔隙比的函数。仵彦卿[42]则将等效裂隙岩体渗透率确定为岩石应力的函数并考虑了应力的方向性。Edip等[43]提出了一种考虑水土保持曲线非线性和固体变形模型的多相耦合模型，岩石的位移和水、气两相的压力都是该模型的变量。热力场、化学场的耦合作用也被添加到渗流-力学场耦合模型中[44-45]，用以研究温度、溶质浓度对固体变形的影响以及多组分沉淀/溶解和离子交换反应在多场耦合中的影响。模型的应用范围不断扩大，目前力学途径模型较新的应用包括多场耦合作用下的地下水污染物迁移、固体废物的深部注入和温室气体的地质封存等[46-48]。
2.2.2 混合耦合理论途径全耦合模型混合耦合理论基于混合理论发展而来[49]，后者最早起源于生物科学领域[50]。混合理论假设所有相态在介质中每一点均匀分布，因此可以对多相混合物使用动量和质量平衡方程[51]，混合理论近年来在地质科学与环境科学领域得到了充分的应用[39, 52-54]。混合理论保持了固体和流体相的独立性，但是很难获得各相之间相互作用的信息。混合耦合理论则克服了这一缺点，以亥姆霍兹自由能为纽带关联不同物理场，以体系内熵产为唯一的驱动力，提供了统一的理论框架。混合耦合理论能够将岩土力学和地球化学联系起来[49]，可以用于建立基于岩土力学和地球化学之间单一统一理论的耦合公式，对流体和固体的多相耦合刻画尤为突出。按照混合耦合理论，一般形式的热力-渗流-力学-化学场耦合模型方程[55-56]为：
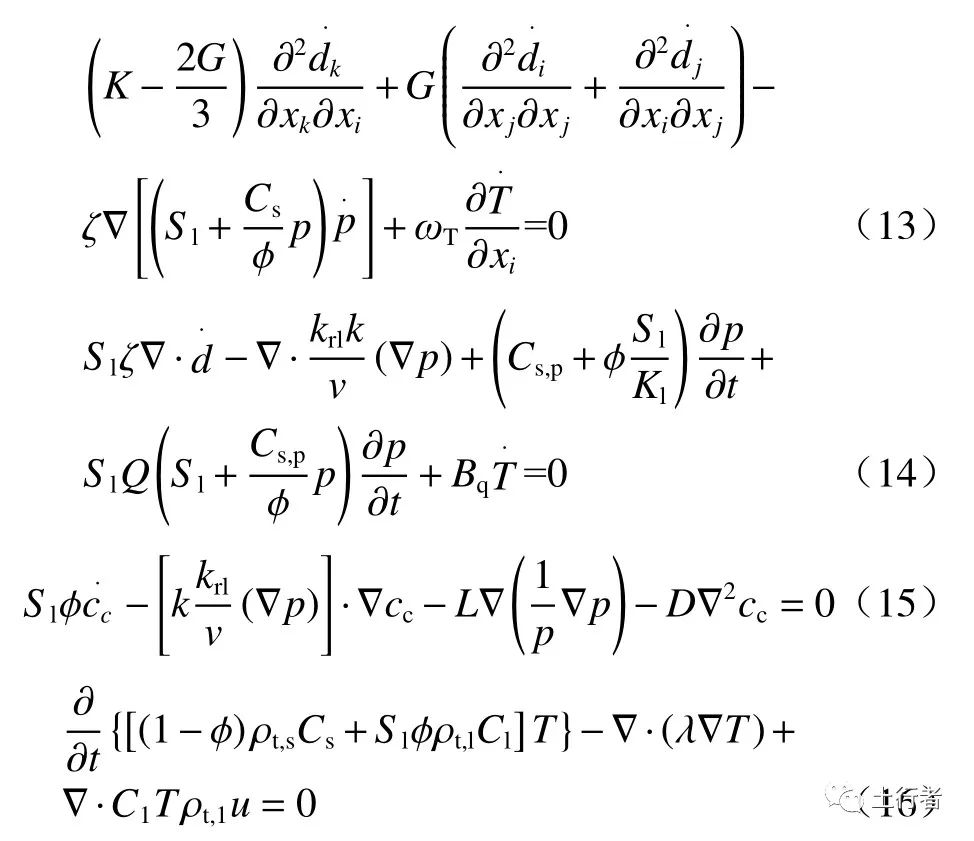
式中：i,j,k=x,y,z；K为岩石体积模量，Pa；d为位移，m；ζ为固结系数；Cs为 固体比热容，m2/(s2·℃)；ωT=βs/3， βs为 固体热膨胀系数，kg/(m·s2·℃) ；Q为与流体压力有关的材料系数，m·s2/kg；Bq为与温度有关的材料系数，kg/(m·s2·℃)；L为压力扩散系数，用以衡量压力对溶质扩散的影响，m2/s；ρt,s为固体密度，ρt,l为 液体密度， kg/m3；Cl为液体比热容，m2/(s2·℃)；λ为热传导系数，m·kg/(s3·℃)；T为温度，℃。式(13)为力学场方程，其中耦合了流体压力与温度变化对于岩石变形的影响。式(14)为渗流场方程，其中耦合了温度、岩石变形对于流体运移的影响。式(15)为化学溶质场方程，其中耦合了渗流场对于溶质迁移的影响，其中不仅包含对流扩散，也包含流体压力梯度对溶质扩散的影响。式(16)为热力场方程，其中耦合了渗流的影响，此外岩石孔隙度也对热传导产生影响；在实际计算中，可通过嵌入其他场参数（如流体动力粘滞系数、流体密度、岩石弹性模量、化学反应速率等）随温度变化的关系式更好地表征温度对多场耦合的影响。求解上述全耦合热力-渗流-力学-化学场耦合模型可以得到地下水水头、溶质浓度在岩石变形、流体运动、溶质扩散、热传输的共同影响下的时空分布。混合耦合理论最初被用于建立渗流-力学场耦合模型，该模型能够确定孔隙度受流体压力与岩石变形的耦合影响，并以亥姆霍兹自由能为工具，解释了岩石吸水膨胀的耦合原理[57-58]。之后Chen等[30]将模型扩展到到渗流-力学-化学场, MA等[59]研究了热力-渗流-力学-化学场耦合，完善了化学渗透、化学反应与岩石渗流-力学-热力场的耦合理论。此外，由于裂隙岩体中孔隙基质的渗透性通常很弱，以往研究者大多倾向于忽略其中的流动。但极低渗透性岩石往往存在膜效应，有研究表明在高岭土、泥质岩中的热渗透通量非常明显，甚至远远超过达西渗透通量[60-61]，因此流体、溶质、热量输运之间的相互耦合关系往往不可忽略。混合耦合理论不需要从其他学科借用方程，即可通过体系内熵产的关系很方便地表示出不同物理场输运定理的耦合关系[55]
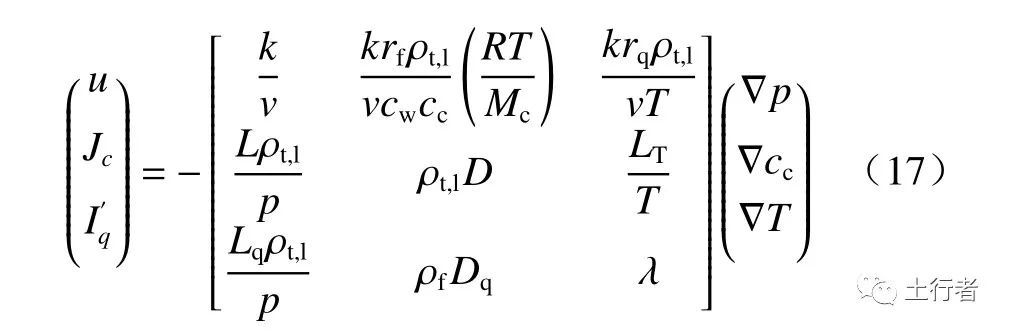
式中：Jc为 溶质扩散通量，kg/(s·m2)；
为热传导通量，kg/s3；r f为化学发射系数，用以衡量化学渗透传输效率，mol2/(m·kg)；cw为 流体中水的质量分数；R为气体 常数，m2·kg/(s2·℃·mol)；Mc为 溶 质 摩尔 质 量，kg/mol；rq为热反射系数，用以衡量热渗透传输效率，m·℃/s2；LT为溶质扩散的热传导系数，用以衡量温度对溶质扩散的影响，kg·℃/(s·m)；Lq为热传导的压力扩散系数，用以衡量压力对热传导的影响，kg·m3/(s5·℃)；Dq为杜弗尔效应系数，表明溶质浓度对热传输的影响，m4/(s3·℃)。不难看出，达西定律、菲克定律、傅里叶热传输定律是在不考虑其他传输现象耦合下的近似。因此，地下水中渗流与溶质迁移现象不仅在均衡方程上受到岩石变形、温度分布的影响，同时流体与溶质的传输也不总是符合简单的输运方程。简化的混合耦合理论途径模型与力学方法得到的结果是一致的。Thomas等[62]对不考虑膨胀、化学与热渗透的情况进行了验证，Chen等[55]对THMC模型的其余特性进行了验证研究，均显示出相比于力学途径较强的优势。
3 讨 论
不同模型概化方法其适用性及优缺点对比见表1。不同的概化方法适用于不同的模拟情景，其具体应用与裂隙分布的均匀程度、水流刻画精度要求、计算量约束等有关。
表1 模型概化方法对比分析
Tab.1 Comparison and analysis of different model conceptual method
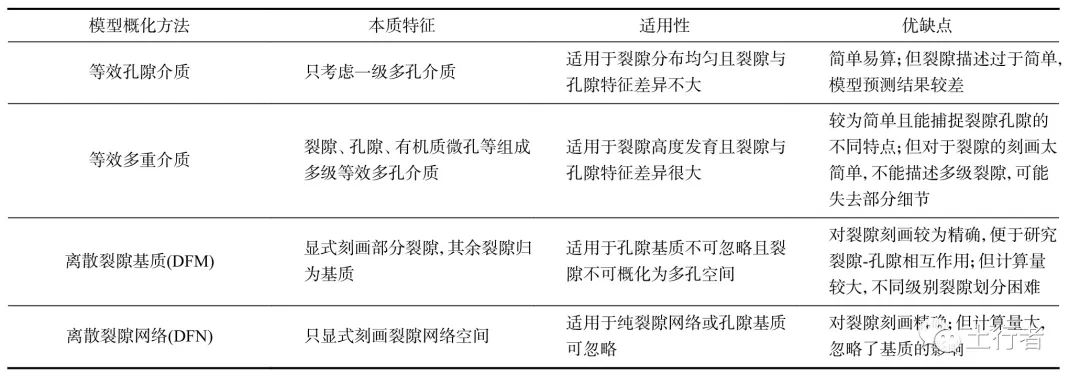
对于多物理场耦合的裂隙水流问题，模型的概化不仅需要考虑到对于水流的刻画精度，同时必须关注不同概化方法对力学场、化学场、热场的影响。全耦合模型能够更加全面地考虑多物理场之间的直接耦合效应，目前正在成为主要的研究手段。由于多物理场耦合研究起源于固结问题，因此早期的多场耦合模型大多基于力学途径，即基于动量守恒和受力平衡的基本理论，通过有效应力建立水压力和固体变形的耦合关系。之后，力学途径模型被扩展到了考虑包括化学反应、热传递、电场影响、生物作用等多个领域。力学途径在处理渗流-岩石力学耦合行为上较为简便。然而，涉及化学溶质研究时，由于岩土力学和地球化学之间的差距，力学方法需要借用地球化学中的化学输运和反应公式[63]，这使得基于力学途径建立的耦合模型在理论框架上欠缺统一性[64]，因为力学途径的控制方程主要来自宏观现象的本构表述。更为重要的是，裂隙介质中存在差异巨大的不同赋存空间，尺度从0.1 nm 到0.1 m，不同尺度中不同相间存在着复杂的耦合作用。地球化学研究一般集中在分子尺度（1 nm及以下尺度）反应[65]，而传统岩土及地下水研究一般集中在大于100 nm的颗粒[66]，在1~100 nm存在两个数量级的知识空缺，具有较强的多尺度物理化学耦合效应，即分子尺度的化学过程可能对宏观物理现象产生强烈的影响。例如低渗透性的孔隙基质可能产生化学渗透流(小至1 nm尺度)，即大分子的溶质较难通过纳米通道而溶剂分子可以通过，这种选择透过性可能强烈影响到岩石的变形（大于0.1 m）。传统的牛顿力学只能于计算液体与固体表面的相互作用，但溶质溶剂之间的分子摩擦超出了牛顿力学的范围，因此必须利用能量途径的理论来解决类似问题。混合耦合理论途径使用了亥姆霍兹自由能和熵产分析，在处理多尺度（例如分子摩擦力和动力学变化）和多物理场耦合上采用基于非平衡热力学的统一方法，由于热力学广泛应用于化学（如化学热力学）和物理（如热力学），混合耦合理论能够很好地建立多尺度多场耦合模型，且模型具有一致性与统一性。虽然其控制方程仍然是满足连续性的宏观表述，但可以更好地表征微观现象（膜效应、溶胀、化学反应等）对多场耦合的影响。裂隙介质中多场耦合研究正不断拓展至新的领域，需要考虑的耦合作用越来越多。虽然关于岩石大变形的基本方程在岩土力学中已经有较充分的研究，但目前考虑岩石大变形的地下水多场耦合模型研究仍然很有限，这种类型的模型研究可能对广泛使用黏土材料的垃圾填埋场、危险废物处理场地的地下水污染模拟研究具有重要意义。李一鸣等[67]和李旭等[68]的研究表明裂隙非达西流对区域流场及污染溶质传输存在影响，如何耦合基质达西流与裂隙非达西流也是一个值得关注的问题。近年来，随着对地下水污染的不断关注，考虑溶质衰减与生物/非生物降解的耦合模型研究正变得越来越重要[69]，熊贵耀等[70]构建了含水层微生物场与水动力场、温度场、化学场耦合的本构模型。不管是孔隙水还是裂隙水中的污染组分，其不仅受到力学-渗流-化学-热力场的共同控制，同时在体系中还存在着多种天然衰减效应与生物/非生物降解作用，然而，地球化学反应和微生物活动常常是一个较长时间尺度的过程，如何耦合不同时间尺度的反应过程是目前生物非生物耦合模型面临的主要困难。
4 展 望
近年来，地下水科学研究领域不断扩展，越来越广的生产实践必然导致对裂隙介质研究的不断深入。将现有数学模型研究按照不同储层空间概化、耦合方式、模型推导方法进行分类，综述裂隙地下水渗流与溶质迁移数学模型的发展历程与阶段性成果。未来裂隙地下水渗流及溶质迁移数学模型的研究方向和研究重点包括：对于裂隙分布的研究与裂隙空间的准确描述。裂隙空间的准确描述是裂隙地下水模拟的重要先决条件，这需要更可靠便捷的地质勘探手段、更先进适用的数据分析方法与平台。对岩石大变形影响下地下水耦合模型的研究。将岩石大变形理论引入裂隙水模型将有助于解决特殊场地特殊工况下的多场耦合问题。考虑溶质衰减与生物/非生物降解的耦合模型研究。考虑反应性溶质的衰减与降解作用的耦合模型将在地下水污染与防治、土壤污染控制与修复等领域得到广泛应用。新的数学模型迫切需要打通微观分子化学-宏观岩石物理学科壁垒，确定地下水中化学、生物、力学等时间尺度差异巨大的耦合作用机制，并优化模型计算方法，提升天然裂隙空间水流与溶质模拟的计算性能。
文章来源：土行者
作者：谭文捷1，王锴2，陈程3，马悦4，司艳晓1，程莉蓉2，陈晓辉4，袁煜旻2，丁爱中2
（1.中石化石油勘探开发研究院 地面工程研究所, 北京102206；2.北京师范大学水科学研究院, 北京 100875；3.中国国际工程咨询有限公司资源与环境业务部, 北京100048；4.利兹大学土木工程学院, 利兹 LS2 9JT, 英国）
